Individual email messages are encrypted via session keys using the Twofish block cipher and ISAAC stream cipher. Each session key is then encrypted with the SecExMail public key for the recipient of the message. Upon receipt of the message, the session key is decrypted via the recipient's private key. Once the session key for the message has been retrieved, the message itself can be decrypted. In order for the message to be secure this session key must be both random and unknowable.
Consider the following scenario where a home owner protects his garden shed with a combination pad lock. Assume further that the brand of pad lock the home owner purchased has four dials, each bearing the digits "1" through "9", and that the dials have a slight tendency to snag on the number "7". If the tendency is slight enough so as to be hardly noticeable many a buyer will, without being aware of this, chose a combination involving one or more sevens. Ordinarily a thief would be compelled to try 10,000 settings in an exhaustive search for the correct combination. On average, therefore, a thief will succeed after 5000 tries. The educated thief, however, knows that all locks of this brand have a tendency to snag on the number "7". If the thief establishes that the first two dials are so affected, then only the second pair of dials is truly unknown. With some luck, the thief only needs to examine 100 combinations, 00..99 on the second pair of dials, in order to open the lock. Our number lock, although it provides for a "key space" of 10,000 combinations has a statistical bias - some combinations are more likely than others. In order for the combination lock to be useful, its combination must be entirely unknowable.
Much the same applies to encryption keys - size does matter. But for a large encryption key to be strong, it must be unknowable to a potential attacker. This requires the input of good random numbers during key generation. If the inputs to the key generation are not random, an attacker will be able to exploit the statistical bias. Why cut the lock, when you can simply dial the correct number ? Good randomness, unfortunately, is difficult to produce for modern computers. Computers are calculating machines which perform predefined operations according to predefined scripts, called programs. Nothing about a computer is random. Computing is 100% deterministic albeit complex and sometimes opaque to the human observer. To compensate for this shortcoming, random number generators accept what is referred to as a seed. The seed initializes the internal state of the random number generator and thus sets a starting point. Thereafter a complex mathematical sequence is applied to produce statistically pattern free output. If the starting point, or seed, to the mathematical sequence is unknowable, the random number generator can be said to be "truly random". This unknowable starting point is referred to as "entropy". The entropy of a system is the measure of its unpredictability.
Because computers are inherently deterministic, the best source of unpredictability is the human user. Many encryption systems make the mistake to digest state information about the computer, such as screen shots or process lists, gathered in short term observations into entropy data. Many encryption tools are confined to gathering entropy in this manner by the nature of their design. An encryption plugin for an email client, for example, is only invoked for a very short period of time when it is asked to asked to encrypt an email message. It is then free to digest short term state information about the computer into entropy. The problem with this approach is that the next invocation will possibly produce similar state information. Thus if little has changed in the computer's state since the last invocation, the entropy collected at each invocation will exhibit a high degree of correlation. Some designs safeguard against this by writing a seed file to disk which transfers state information from one invocation to the next. However, the amount of entropy gathered by a program which only exists in computer memory for but a brief time is inherently limited.
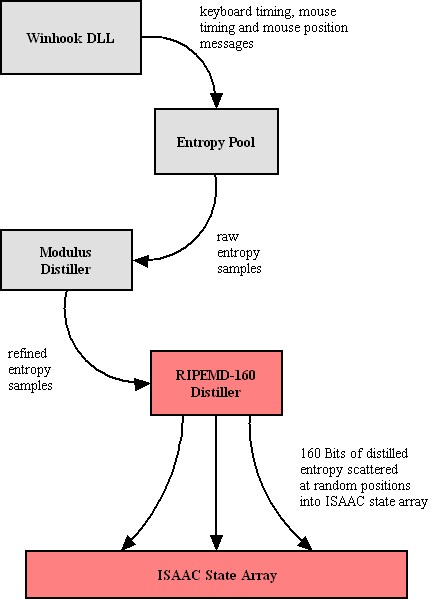
For this reason, and to mine the entropy which may be found in the interaction between the human user and the computer, SecExMail operates an entropy collection subsystem which runs continuously during the operation of the computer, even when no email is being sent or received. The entropy collection extracts unknowable user data and re-seeds small subsections of the random number generator's state array as entropy data becomes available. A perfect source of randomness are keyboard timings and mouse clicks, mouse movements and mouse timings. The entropy collection subsystem NEVER records your keystrokes or any other user information, but exploits the timing information contained in system events generated by the user. Since some users tend to be slower typists than others, and yet other users make predominant use of the mouse, SecExMail uses two strategies to distill "unknowability" from the data it collects.
1) Modulus Calculation
The modulus operation is a mathematical calculation which computes the remainder of integer division. For example 7 MOD 3 equals 1. Perhaps you recall this kind of arithmetic from "Kindergarten Math". "How often does 3 go into 7 ?" Answer 2, remainder 1. This kind of arithmetic is useful in removing bias from nearly random data. For example one might conduct a survey recording the height of shoppers in a mall. When asking "random" adults how tall they are, the answers are likely to fall into a certain range : 5 foot 9, 6 foot 1, 5 foot 11, etc. While the exact answers will be unknowable to someone who did not accompany the surveyor, the collected data will not be entirely unknowable as the majority of answers will fall into a certain range. However, consider what happens when we compute the "modulus 3" of the above values.
Regardless of the ethnicity of the population surveyed, someone who did not accompany the surveyor will be unable to predict the sequence of zeroes, ones and twos which will emerge. The average height of the examined population is biased, but whether a population member's height is an integral multiple of 3 inches is entirely unknowable.
2) Secure Hash Functions
The second strategy employed by the entropy collection subsystem to distill randomness from biased data is to apply a secure hash function. Secure, one way hash functions are used for digital signatures and cryptographic checksums. According to Ron Rivest, one of the designers of RSA encryption, hash functions are designed such that "It is computationally infeasible to find two messages that hashed to the same value. No attack is more efficient than brute force." As such, hash functions tend to preserve the smallest differences in a sample and have the added property of preserving the entropy found in the sample. It is important to note that SecExMail does not use secure hash functions to "stretch" the randomness in small data sets, but to distill the entropy in data pools containing hundreds or thousands of data items to 160 bits of entropy. SecExMail employs the RIPEMD-160 message digest.
Entropy is gathered in entropy pools, distilled as described above and finally scattered randomly into the state array of the ISAAC random number generator. The diagram shown below depicts the flow of data in the entropy collection subsystem.
To prevent attacks on the random number generator based on the monitoring of key strokes and mouse events by third parties, the SecExMail entropy collection does not employ event timings which represent times at which the operating system recorded the events, but instead uses internal timestamps which represent the times at which the events were recorded by SecExMail's own message queue. This message queue is subject to further timing distortions by other events and the general multitasking behavior of the application. |