Previous  Top  Next

Windows Time Server

Appendix E

The NTP Timescale and its Chronometry

Introduction

Following is an extended discussion on computer network chronometry, which is the precise determination of computer time and frequency relative to international standards and the determination of conventional civil time and date according to the modern calendar. It describes the methods conventionally used to establish civil time and date and the various timescales now in use. In particular, it characterizes the Network Time Protocol (NTP) time scale relative to the Coordinated Universal Time (UTC) time scale, and establishes the precise interpretation of UTC leap seconds in NTP.

In the following discussion the terms time, oscillator, clock, epoch, calendar, date and time scale are used in a technical sense. Strictly speaking, the time of an event is an abstraction which determines the ordering of events in some given frame of reference. An oscillator is a generator capable of precise frequency (relative to the given frame of reference) to a specified tolerance. A clock is an oscillator together with a counter which records the (fractional) number of cycles since being initialized with a given value at a given time. The value of the counter at any given time is called its epoch at that time. In general, epoches are not continuous and depend on the precision of the counter.

A calendar is a mapping from epoch in some frame of reference to the times and dates used in everyday life. Since multiple calendars are in use today and sometimes disagree on the dating of the same events in the past, the chronometry of past and present events is an art practiced by historians. One of the goals of this discussion is to provide a standard chronometry for precision dating of present and future events in a global networking community. To synchronize frequency means to adjust the oscillators in the network to run at the same frequency, to synchronize time means to set the clocks so that all agree at a particular epoch with respect to UTC, as provided by international standards, and to synchronize clocks means to synchronize them in both frequency and time.

In order to synchronize clocks, there must be some way to directly or indirectly compare them in time and frequency. The ultimate frame of reference for our world consists of the cosmic oscillators: the Sun, Moon and other galactic orbiters. Since the frequencies of these oscillators are relatively unstable and not known exactly, the ultimate reference standard oscillator has been chosen by international agreement as a synthesis of many observations of an atomic transition of exquisite stability. The epoches of each heavenly and Earthbound oscillator defines a distinctive time scale, not necessarily always continuous, relative to the standard oscillator. Another goal of this presentation is to describe a standard chronometry to rationalize conventional computer time and UTC; in particular, how to handle leap seconds.

Primary Frequency and Time Standards

A primary frequency standard is an oscillator that can maintain extremely precise frequency relative to a physical phenomenon, such as a transition in the orbital states of an electron. Presently available atomic oscillators are based on the transitions of the hydrogen, cesium and rubidium atoms. Table

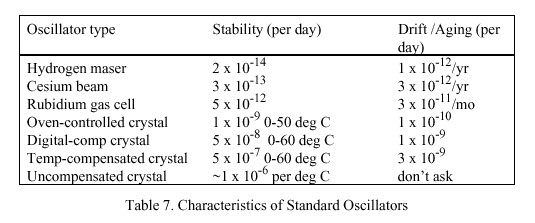
7 shows the characteristics for typical oscillators of these types compared with those for various types of quartz-crystal oscillators found in electronic equipment. For reasons of cost and robustness cesium oscillators are used worldwide for national primary frequency standards. On the other hand, local clocks used in computing equipment almost always are designed with uncompensated crystal oscillators.

For the three atomic oscillators listed in Table 7 the drift/aging column shows the maximum offset per day from nominal standard frequency due to systematic mechanical and electrical characteristics. In the case of crystal oscillators this offset is not constant, which results in a gradual change in frequency with time, called aging. Even if a crystal oscillator is temperature compensated by some means, it must be periodically compared to a primary standard in order to maintain the highest accuracy. For all types of oscillators the stability column shows the maximum variation in frequency per day due to circuit noise and environmental factors.

As the telephone networks of the world are evolving rapidly to digital technology, consideration should be given to the methods used for frequency synchronization in digital networks. A network of clocks in which each oscillator is phase-locked to a single frequency standard is called isochronous, while a network in which some oscillators are phase-locked to different master oscillators, but with the master oscillators closely synchronized in frequency (not necessarily phase locked), to a single frequency standard is called plesiochronous. In plesiochronous systems the phase of some oscillators can slip relative to others and cause occasional data errors in synchronous transmission systems.

The industry has agreed on a classification of clock oscillators as a function of minimum accuracy, minimum stability and other factors [ALL74a]. There are three factors which determine the classification: stability, jitter and wander. Stability refers to the systematic variation of frequency with time and is synonymous with aging, drift, trends, etc. Jitter (also called timing jitter) refers to short-term variations in frequency with components greater than 10 Hz, while wander refers to long-term variations in frequency with components less than 10 Hz. The classification determines the oscillator stratum (not to be confused with the NTP stratum), with the more accurate oscillators assigned the lower strata and less accurate oscillators the higher strata:



The construction, operation and maintenance of stratum-one oscillators is assumed to be consistent with national standards and often includes cesium oscillators or precision crystal oscillators synchronized via LORAN-C to national standards. Stratum-two oscillators represent the stability required for interexchange toll switches such as the AT&T 4ESS and interexchange digital cross-connect systems, while stratum-three oscillators represent the stability required for exchange switches such as the AT&T 5ESS and local cross-connect systems. Stratum-four oscillators represent the stability required for digital channel-banks and PBX systems.

Time and Frequency Dissemination

In order that atomic and civil time can be coordinated throughout the world, national administrations operate primary time and frequency standards and coordinate them cooperatively by observing various radio broadcasts and through occasional use of portable atomic clocks. Most seafaring nations of the world operate some sort of broadcast time service for the purpose of calibrating chronographs, which are used in conjunction with ephemeris data to determine navigational position. In many countries the service is primitive and limited to seconds-pips broadcast by marine communication stations at certain hours. For instance, a chronograph error of one second represents a longitudinal position error of about 0.23 nautical mile at the Equator.

The U.S. National Institute of Standards and Technology (NIST - formerly National Bureau of Standards) operates three radio services for the dissemination of primary time and frequency information. One of these uses high-frequency (HF or CCIR band 7) transmissions on frequencies of 2.5, 5, 10, 15 and 20 MHz from Fort Collins, CO (WWV), and Kauai, HI (WWVH). Signal propagation is usually by reflection from the upper ionospheric layers, which vary in height and composition throughout the day and season and result in unpredictable delay variations at the receiver. The timecode is transmitted over a 60-second interval at a data rate of 1 bps using a 100-Hz subcarrier on the broadcast signal. The timecode information includes UTC time-day information, but does not currently include year or leap-second warning. While these transmissions and those of Canada from Ottawa, Ontario (CHU), and other countries can be received over large areas in the western hemisphere, reliable frequency comparisons can be made only to the order of 10-7 and time accuracies are limited to the order of a millisecond [BLA74]. Radio clocks which operate with these transmissions include the Traconex 1020, which provides accuracies to about ten milliseconds and is priced in the $1,500 range.

A second service operated by NIST uses low-frequency (LF or CCIR band 5) transmissions on 60 kHz from Boulder, CO (WWVB), and can be received over the continental U.S. and adjacent coastal areas. Signal propagation is via the lower ionospheric layers, which are relatively stable and have predictable diurnal variations in height. The timecode is transmitted over a 60-second interval at a rate of 1 pps using periodic reductions in carrier power. With appropriate receiving and averaging techniques and corrections for diurnal and seasonal propagation effects, frequency comparisons to within 10-11 are possible and time accuracies of from a few to 50 microseconds can be obtained [BLA74]. Some countries in western Europe operate similar services which use transmissions on 60 kHz from Rugby, U.K. (MSF), and on 77.5 kHz from Mainflingen, West Germany (DCF77). The timecode information includes UTC time-day-year information and leap-second warning. Radio clocks which operate with these transmissions include the Spectracom 8170 and Kinemetrics/TrueTime 60-DC and LF-DC, which provide accuracies to a millisecond or less and are priced in the $2,500 range. However, these receivers do not extract the year information and leap-second warning.

The third service operated by NIST uses ultra-high frequency (UHF or CCIR band 9) transmissions on about 468 MHz from the Geosynchronous Orbit Environmental Satellites (GOES), three of which cover the western hemisphere. The timecode is interleaved with messages used to interrogate remote sensors and consists of 60 4-bit binary-coded decimal words transmitted over an interval of 30 seconds. The timecode information includes UTC time-day-year information and leap-second warning. Radio clocks which operate with these transmissions include the Kinemetrics/TrueTime 468-DC, which provides accuracies to 0.5 ms and is priced in the $6,000 range. However, this receiver does not extract the year information and leap-second warning.

The U.S. Department of Defense is developing the Global Positioning System (GPS) for worldwide precision navigation. This system will eventually provide 24-hour worldwide coverage using a constellation of 24 satellites in 12-hour orbits. For time-transfer applications GPS has a potential accuracy in the order of a few nanoseconds; however, various considerations of defense policy may limit accuracy to hundreds of nanoseconds [VAN84]. The timecode information includes GPS time and UTC correction; however, there appears to be no leap-second warning. Radio clocks which operate with these transmissions include the Kinemetrics/TrueTime GPS-DC, which provides accuracies to 200 <$Emu>s and is priced in the $12,000 range. However, since only about half the satellites have been launched, expensive rubidium or quartz oscillators are necessary to preserve accuracy during outages. Also, since this is a single-channel receiver, it must be supplied with geographic coordinates within a degree from an external source before operation begins.

The U.S. Coast Guard, along with agencies of other countries, has operated the LORAN-C [FRA82] radionavigation system for many years. It currently provides time-transfer accuracies of less than a microsecond and eventually may achieve 100 ns within the ground-wave coverage area of a few hundred kilometers from the transmitter. Beyond the ground wave area signal propagation is via the lower ionospheric layers, which decreases accuracies to the order of 50 us. With the recent addition of the Mid-Continent Chain, the deployment of LORAN-C transmitters now provides complete coverage of the U.S. LORAN-C timing receivers, such as the Austron 2000, are specialized and extremely expensive (up to $20,000). They are used primarily to monitor local cesium clocks and are not suited for unattended, automatic operation. While the LORAN-C system provides a highly accurate frequency and time reference within the ground wave area, there is no timecode modulation, so the receiver must be supplied with UTC time to within a few tens of seconds from an external source before operation begins.

The OMEGA [VAS78] radionavigation system operated by the U.S. Navy and other countries consists of eight very-low-frequency (VLF or CCIR band 4) transmitters operating on frequencies from 10.2 to 13.1 kHz and providing 24-hour worldwide coverage. With appropriate receiving and averaging techniques and corrections for propagation effects, frequency comparisons and time accuracies are comparable to the LF systems, but with worldwide coverage [BLA74]. Radio clocks which operate with these transmissions include the Kinemetrics/TrueTime OM-DC, which provides accuracies to 1 ms and is priced in the $3,500 range. While the OMEGA system provides a highly accurate frequency reference, there is no timecode modulation, so the receiver must be supplied with geographic coordinates within a degree and UTC time within five seconds from an external source before operation begins. There are several other VLF services intended primarily for worldwide data communications with characteristics similar to OMEGA. These services can be used in a manner similar to OMEGA, but this requires specialized techniques not suited for unattended, automatic operation.

Note that not all transmission formats used by NIST radio broadcast services [NBS79] and no currently available radio clocks include provisions for year information and leap-second warning. This information must be determined from other sources. NTP includes provisions to distribute advance warnings of leap seconds using the leap-indicator bits described in the NTP specification. The protocol is designed so that these bits can be set manually or by the radio timecode at the primary time servers and then automatically distributed throughout the synchronization subnet to all other time servers.

Calendar Systems

The calendar systems used in the ancient world reflect the agricultural, political and ritual needs characteristic of the societies in which they flourished. Astronomical observations to establish the winter and summer solstices were in use three to four millennia ago. By the 14th century BC the Shang Chinese had established the solar year as 365.25 days and the lunar month as 29.5 days. The lunisolar calendar, in which the ritual month is based on the Moon and the agricultural year on the Sun, was used throughout the ancient Near East (except Egypt) and Greece from the third millennium BC. Early calendars used either thirteen lunar months of 28 days or twelve alternating lunar months of 29 and 30 days and haphazard means to reconcile the 354/364-day lunar year with the 365-day vague solar year.

The ancient Egyptian lunisolar calendar had twelve 30-day lunar months, but was guided by the seasonal appearance of the star Sirius (Sothis). In order to reconcile this calendar with the solar year, a civil calendar was invented by adding five intercalary days for a total of 365 days. However, in time it was observed that the civil year was about one-fourth day shorter than the actual solar year and thus would precess relative to it over a 1460-year cycle called the Sothic cycle. Along with the Shang Chinese, the ancient Egyptians had thus established the solar year at 365.25 days, or within about 11 minutes of the present measured value. In 432 BC, about a century after the Chinese had done so, the Greek astronomer Meton calculated there were 110 lunar months of 29 days and 125 lunar months of 30 days for a total of 235 lunar months in 6940 solar days, or just over 19 years. The 19-year cycle, called the Metonic cycle, established the lunar month at 29.532 solar days, or within about two minutes of the present measured value.

The Roman republican calendar was based on a lunar year and by 50 BC was eight weeks out of step with the solar year. Julius Caesar invited the Alexandrian astronomer Sosigenes to redesign the calendar, which led to the adoption in 46 BC of the Julian calendar. This calendar is based on a year of 365 days with an intercalary day inserted every four years. However, for the first 36 years an intercalary day was mistakenly inserted every three years instead of every four. The result was 12 intercalary days instead of nine, and a series of corrections that was not complete until 8 AD.

The seven-day Sumerian week was introduced only in the fourth century AD by Emperor Constantine I. During the Roman era a 15-year census cycle, called the Indiction cycle, was instituted for taxation purposes. The sequence of day-names for consecutive occurrences of a particular day of the year does not recur for 28 years, called the solar cycle. Thus, the least common multiple of the 28-year solar cycle, 19-year Metonic cycle and 15-year Indiction cycle results in a grand 7980-year supercycle called the Julian Era, which began in 4713 BC. A particular combination of the day of the week, day of the year, phase of the Moon and round of the census will recur beginning in 3268 AD.

By 1545 the discrepancy in the Julian year relative to the solar year had accumulated to ten days. In 1582, following suggestions by the astronomers Christopher Clavius and Luigi Lilio, Pope Gregory XIII issued a papal bull which decreed, among other things, that the solar year would consist of 365.2422 days. In order to more closely approximate the new value, only those centennial years divisible by 400 would be leap years, while the remaining centennial years would not, making the actual value 365.2425, or within about 26 seconds of the current measured value. Since the beginning of the Common Era and prior to 1990 there were 474 intercalary days inserted in the Julian calendar, but 14 of these were removed in the Gregorian calendar. While the Gregorian calendar is in use throughout most of the world today, some countries did not adopt it until early in the twentieth century. While it remains a fascinating field for time historians, the above narrative provides conclusive evidence that conjugating calendar dates of significant events and assigning NTP timestamps to them is approximate at best. In principle, reliable dating of such events requires only an accurate count of the days relative to some globally alarming event, such as a comet passage or supernova explosion; however, only historically persistent and politically stable societies, such as the ancient Chinese and Egyptian, and especially the classic Maya, possessed the means and will to do so.

The Modified Julian Day System

In order to measure the span of the universe or the decay of the proton, it is necessary to have a standard day-numbering plan. Accordingly, the International Astronomical Union has adopted the use of the standard second and Julian Day Number (JDN) to date cosmological events and related phenomena. The standard day consists of 86,400 standard seconds, where time is expressed as a fraction of the whole day, and the standard year consists of 365.25 standard days.

In the scheme devised in 1583 by the French scholar Joseph Julius Scaliger and named after his father, Julius Caesar Scaliger, JDN 0.0 corresponds to 12h (noon) on the first day of the Julian Era, 1 January 4713 BC. The years prior to the Common Era (BC) are reckoned according to the Julian calendar, while the years of the Common Era (AD) are reckoned according to the Gregorian calendar. Since 1 January 1 AD in the Gregorian calendar corresponds to 3 January 1 in the Julian calendar [DER90], JDN 1,721,426.0 corresponds to 12h on the first day of the Common Era, 1 January 1 AD. The Modified Julian Date (MJD), which is sometimes used to represent dates near our own era in conventional time and with fewer digits, is defined as MJD = JD <196> 2,400,000.5. Following the convention that our century began at 0h on 1 January 1900, at which time the tropical year was already 12h old, that eclectic instant corresponds to MJD 15,020.0. Thus, the Julian time scale ticks in standard (atomic) 365.25-day centuries and was set to a given value at the approximate epoch of a cosmic event which apparently synchronized the entire human community, the origin of the Common Era.

Determination of Frequency

For many years the most important use of time and frequency information was for worldwide navigation and space science, which depend on astronomical observations of the Sun, Moon and stars [JOR85]. Sidereal time is based on the transit of stars across the celestial meridian of an observer. The mean sidereal day is 23 hours, 56 minutes and 4.09 seconds, but varies about <F128M>æ<F255D>30 ms throughout the year due to polar wandering and orbit variations. Ephemeris time is based on tables with which a standard time interval such as the tropical year - one complete revolution of the Earth around the Sun - can be determined through observations of the Sun, Moon and planets. In 1958 the standard second was defined as 1/31,556,925.9747 of the tropical year that began this century. On this scale the tropical year is 365.2421987 days and the lunar month - one complete revolution of the Moon around the Earth - is 29.53059 days; however, the actual tropical year can be determined only to an accuracy of about 50 ms and has been increasing by about 5.3 ms per year.

Of the three heavenly oscillators readily apparent to ancient mariners and astronomers - the Earth rotation about its axis, the Earth revolution around the Sun and the Moon revolution around the Earth - none of the three have the intrinsic stability, relative to modern technology, to serve as a standard reference oscillator. In 1967 the standard second was redefined as <169>9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom.<170> Since 1972 the time and frequency standards of the world have been based on International Atomic Time (TAI), which is defined and maintained using multiple cesium-beam oscillators to an accuracy of a few parts in 1013, or better than a microsecond per day. Note that, while this provides an extraordinarily precise time scale, it does not necessarily agree with conventional solar time and may not in fact even be absolutely uniform, unless subtle atomic conspiracies can be ruled out.

Determination of Time and Leap Seconds

The International Bureau of Weights and Measures (IBWM) uses astronomical observations provided by the U.S. Naval Observatory and other observatories to determine UTC. Starting from apparent mean solar time as observed, the UT0 time scale is determined using corrections for Earth

orbit and inclination (the Equation of Time, as used by sundials), the UT1 (navigator's) time scale by adding corrections for polar migration and the UT2 time scale by adding corrections for known periodicity variations. While standard frequencies are based on TAI, conventional civil time is based on UT1, which is presently slowing relative to TAI by a fraction of a second per year. When the magnitude of correction approaches 0.7 second, a leap second is inserted or deleted in the TAI time scale on the last day of June or December.

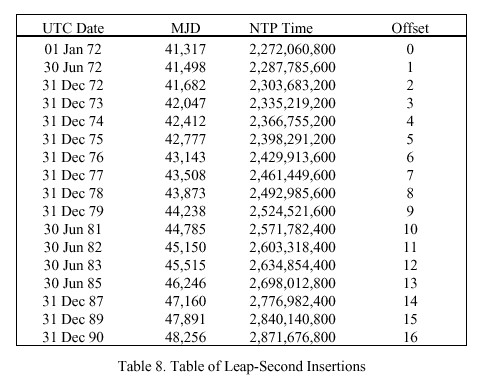
For the most precise coordination and time stamping of events since 1972, it is necessary to know when leap seconds are implemented in UTC and how the seconds are numbered. As specified in CCIR Report 517, which is reproduced in [BLA74], a leap second is inserted following second 23:59:59 on the last day of June or December and becomes second 23:59:60 of that day. A leap second would be deleted by omitting second 23:59:59 on one of these days, although this has never happened. Leap seconds were inserted prior to 1 January 1991 on the occasions listed in Table 8<$&tab8> (courtesy U.S. Naval Observatory). Published IBWM corrections consist not only of leap seconds, which result in step discontinuities relative to TAI, but 100-ms UT1 adjustments called DUT1, which provide increased accuracy for navigation and space science.

Note that the NTP time column actually shows the epoch following the last second of the day given in the UTC date and MJD columns (except for the first line), which is the precise epoch of insertion. The offset column shows the cumulative seconds offset between the uncoordinated (Julian) time scale and the UTC time scale; that is, the number of seconds to add to the Julian clock in order to maintain nominal agreement with the UTC clock. Finally, note that the epoch of insertion is relative to the time scale immediately prior to that epoch; e.g., the epoch of the 31 December 90 insertion is determined on the time scale in effect following the 31 December 1990 insertion, which means the actual insertion relative to the Julian clock is fourteen seconds later than the apparent time on the UTC time scale.

The UTC time scale thus ticks in standard (atomic) seconds and was set to the value 0h MJD 41,317.0 at the epoch determined by astronomical observation to be 0h on 1 January 1972 according to the Gregorian calendar; that is, the inaugural tick of the UTC Era. In fact, the inaugural tick which synchronized the cosmic oscillators, Julian clock, UTC clock and Gregorian calendar forevermore was displaced about ten seconds from the civil clock then in use, while the GPS clock is ahead of the UTC clock by six seconds in late 1990. Subsequently, the UTC clock has marched backward relative to the Julian time scale exactly one second on scheduled occasions at monumental epoches embedded in the institutional memory of our civilization. Note in passing that leap-second adjustments affect the number of seconds per day and thus the number of seconds per year. Apparently, should we choose to worry about it, the UTC clock, Julian clock and various cosmic clocks will inexorably drift apart with time until rationalized by some future papal bull.

The NTP Timescale and Reckoning with UTC The NTP time scale is based on the UTC time scale, but not necessarily always coincident with it. At 0h on 1 January 1972 (MJD 41,317.0), the first tick of the UTC Era, the NTP clock was set to 2,272,060,800, representing the number of standard seconds since 0h on 1 January 1900 (MJD 15,020.0). The insertion of leap seconds in UTC and subsequently into NTP does not affect the UTC or NTP oscillator, only the conversion to conventional civil UTC time. However, since the only institutional memory available to NTP are the UTC timecode broadcast services, the NTP time scale is in effect reset to UTC as each timecode is received. Thus, when a leap second is inserted in UTC and subsequently in NTP, knowledge of all previous leap seconds is lost.

Another way to describe this is to say there are as many NTP timescales as historic leap seconds. In effect, a new time scale is established after each new leap second. Thus, all previous leap seconds, not to mention the apparent origin of the time scale itself, lurch backward one second as each new time scale is established. If a clock synchronized to NTP in 1990 was used to establish the UTC epoch of an event that occurred in early 1972 without correction, the event would appear fifteen seconds late relative to UTC. However, NTP primary time servers resolve the epoch using the broadcast timecode, so that the NTP clock is set to the broadcast value on the current time scale. As a result, for the most precise determination of epoch relative to the historic UTC clock, the user must subtract from the apparent NTP epoch the offsets shown in Table 8 at the relative epoches shown. This is a feature of almost all present day time-distribution mechanisms.

The chronometry involved can be illustrated with the help of Figure 8, which shows the details of seconds numbering just before, during and after the last scheduled leap insertion at 23:59:59 on 31 December 1989. Notice the NTP leap bits are set on the day prior to insertion, as indicated by the <169>+<170> symbols on the figure. Since this makes the day one second longer than usual, the NTP day rollover will not occur until the end of the first occurrence of second 800. The UTC time conversion routines must notice the apparent time and the leap bits and handle the time scale conversions accordingly. Immediately after the leap insertion both timescales resume ticking the seconds as if

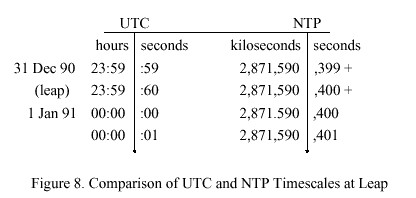
the leap had never happened. The chronometric correspondence between the UTC and NTP timescales continues, but NTP has forgotten about all past leap insertions. In NTP chronometric determination of UTC time intervals spanning leap seconds will thus be in error, unless the exact times of insertion are known.

It is possible that individual systems may use internal data formats other than the NTP timestamp format, which is represented in seconds to a precision of about 200 picoseconds; however, a persuasive argument exists to use a two-part representation, one part for whole days (MJD or some fixed offset from it) and the other for the seconds (or some scaled value, such as milliseconds). This not only facilitates conversion between NTP and conventional civil time, but makes the insertion of leap seconds much easier. All that is required is to change the modulus of the seconds counter, which on overflow increments the day counter. This design insures that continuity of the time scale is assured, even if outside synchronization is lost before, during or after leap-second insertion. Since timestamp data are unaffected, synchronization is assured, even if timestamp data are in flight at the instant and
originated before or at that instant.